软件理论基础与实践
持续更新中......
一. Coq函数式编程
程序语言:
命令式语言:直接描述底层机器应该执行的动作
函数式语言:
𝜆演算:计算的本质是函数调用
采用函数调用描述计算
逻辑式语言:
用户给出前提、结论和推导式
从 前提 推导 结论 的过程就构成了计算
Coq与Gallina:
Coq是一个交互式定理证明工具
Gallina是包含在Coq中的描述语言,是函数式编程语言、也用来描述定理和证明
枚举:
定义一个数据集合Type:
Inductive day : Type := | monday | tuesday | wednesday | thursday | friday | saturday | sunday.函数定义:
Definition next_weekday (d:day) : day := match d with | monday ⇒ tuesday | tuesday ⇒ wednesday | wednesday ⇒ thursday | thursday ⇒ friday | friday ⇒ monday | saturday ⇒ monday | sunday ⇒ monday end.检验:
compute指令:
Eval compute in (next_weekday friday).Eval compute in (next_weekday (next_weekday saturday)).f a表示把a作为参数传给f
空格左结合:f a b = (f a)b
空格的优先级大于其他操作
定理和证明:
Example test_next_weekday: (next_weekday (next_weekday saturday)) = tuesday. Proof. simpl. reflexivity. Qed.Example:声明定理
simpl:化简表达式
reflexivity:根据对称性证明
让 Coq 从 Definition 中'提取(Extract)' 出用其它更加常规的编程语言编写的程序 (如 OCaml、Scheme、Haskell 等)
布尔值:
Inductive bool : Type := | true | false.Definition orb (b1:bool) (b2:bool) : bool := match b1 with | true ⇒ true | false ⇒ b2 end.Notation:为既有的定义赋予新的符号记法,比如以下定义函数orb记法为 ||
Notation "x || y" := (orb x y).条件判断:
Definition orb' (b1:bool) (b2:bool) : bool := if b1 then true else b2.coq支持对任意表达式使用if
类型:
check true. 会返回true是bool类型
check true : bool. 会返回true是不是布尔类型,不是则报错
check negb : bool -> bool.
理解为nega类型是"给定一个 bool 类型的输入,该函数产生一个 bool 类型的输出"
又比如andb 的类型写作 bool → bool → bool,可以理解为 “给定两个 bool 类型的输入,该函数产生一个 bool 类型的输出。”
由旧类型构造新类型:
Inductive rgb : Type := | red | green | blue. Inductive color : Type := | black | white | primary (p : rgb).原子标识符,构造子Constructo:比如之前的true、monday
每个归纳定义的类型(如 day、bool、rgb、color 等) 都描述了一组由'构造子'构成的'构造子表达式' constructor expression。
若 p 是属于 rgb 的构造子表达式,则 primary p(读作“构造子 primary 应用于参数 p)是属于集合 color 的构造子表达式;且通过这些方式构造的构造子表达式'只属于'集合 rgb 和 color。
使用带参数的构造函数:
Definition isred (c : color) : bool := match c with | black ⇒ false | white ⇒ false | primary red ⇒ true | primary _ ⇒ false end.primary _ 是“构造子 primary 应用到除 red 之外的任何 rgb 构造子上”的简写形式
元组:
一个多参数的单构造子可以用来创建元组类型
Inductive bit : Type := | B0 | B1. Inductive nybble : Type := | bits (b0 b1 b2 b3 : bit).运用了包装作用,nybble是一个四比特元组
解包可以通过模式匹配实现:
Definition all_zero (nb : nybble) : bool := match nb with | (bits B0 B0 B0 B0) ⇒ true | (bits _ _ _ _) ⇒ false end.模块:类似于java里的包或c++里的namespace
如果我们将一组定义放在 Module X 和 End X 标记之间,那么在文件中的 End 之后,我们就可以通过像 X.foo 这样的名字来引用,而不必直接用 foo 了
数值:
之前定义的都是有限集合,定义自然数:
皮亚诺公理:
• 0是自然数
• 每个自然数有一个后继,后继也是自然数
• 0不是任何数的后继
• 如果x和y的后继相同,那么x和y相等
定义自然数:
Inductive nat : Type := | O | S (n : nat).0 被表示为 O, 1 则被表示为 S O, 2 则是 S (S O),以此类推
前驱函数:
Definition pred (n : nat) : nat := match n with | O ⇒ O | S n' ⇒ n' end.Coq原生自然数类型:一进制:
Check (S (S (S (S O)))). (* ===> 4 : nat *)需要强调Coq并没有将自然数转换成计算机内部表示 并采用相应汇编指令来计算的过程,这个特性使得包含某些未知量时也能计算,在证明 时非常有用:比如
minustwo (S (S n)) = n定义递归函数:
Fixpoint evenb (n:nat) : bool := match n with | O ⇒ true | S O ⇒ false | S (S n') ⇒ evenb n' end.多参数也可以这样定义:
Fixpoint mult (n m : nat) : nat :=定义减法:
这里使用了并列匹配
Fixpoint minus (n m:nat) : nat := match n, m with | O , _ ⇒ O | S _ , O ⇒ n | S n', S m' ⇒ minus n' m' end.嵌套match:
Fixpoint eqb (n m : nat) : bool := match n with | O ⇒ match m with | O ⇒ true | S m' ⇒ false end | S n' ⇒ match m with | O ⇒ false | S m' ⇒ eqb n' m' end end.结构递归:递归调用的实参是原形参的子结构,一定终止
基于化简的证明:
Theorem plus_O_n' : ∀ n : nat, 0 + n = n. Proof. intros n. reflexivity. Qed.使用 simpl 来化简等式两边,然后用 reflexivity 来检查两边是否具有相同的值。
simpl 策略用于应用乘法的定义并简化等式,使得我们可以看到表达式的具体形式。
reflexivity 策略用于证明等式成立,当两边的表达式完全相同时
关键字 Example 和 Theorem(以及其它一些,包括 Lemma、Fact 和 Remark)都表示完全一样的东西
量词:使用intros n实现“'假设' 存在一个任意自然数 n...”(也可以用别的字母)
关键字 intros、simpl 和 reflexivity 都是'策略(Tactic)'的例子。 策略是一条可以用在 Proof(证明)和 Qed(证毕)之间的指令,它告诉 Coq 如何来检验我们所下的一些断言的正确性
基于改写的证明:
->蕴含
Theorem plus_id_example : ∀ n m:nat, n = m → n + n = m + m.我们需要在能够假定存在自然数 n 和 m 的基础上进行推理。 另外我们需要假定有前提 n = m。intros 策略用来将这三条前提从证明目标 移到当前上下文的假设中:
Proof. (* 将两个量词移到上下文中: *) intros n m. (* 将前提移到上下文中: *) intros H. (* 用前提改写目标: *) rewrite → H. reflexivity. Qed.第三行告诉 Coq 改写当前目标(n + n = m + m),把前提等式 H 的左边替换成右边。
rewrite 中的箭头与蕴含无关:它指示 Coq 从左往右地应用改写。 若要从右往左改写,可以使用 rewrite <-
例:
Theorem plus_id_exercise : forall n m o : nat, n = m -> m = o -> n + m = m + o. Proof. intros n m o H1 H2. (* 引入前提 *) rewrite -> H1. (* 使用等号的传递性,将 n 替换为 m *) rewrite <- H2. (* 使用等号的传递性,将 o 替换为 m *) reflexivity. (* 结论成立 *) Qed.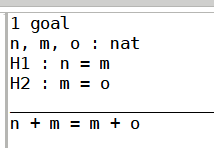
使用分类讨论来证明
Theorem plus_1_neq_0 : ∀ n : nat, (n + 1) =? 0 = false. Proof. intros n. destruct n as [| n'] eqn:E. - reflexivity. - reflexivity. Qed.destruct 策略会生成两个子目标
as [| n'] 这种标注被称为 '引入模式'。它告诉 Coq 应当在每个子目标中 使用什么样的变量名。总体而言,在方括号之间的是一个由 | 隔开的 '列表的列表'(译者注:list of lists)。在上面的例子中,第一个元素是 一个空列表,因为 O 构造子是一个空构造子(它没有任何参数)。 第二个元素提供了包含单个变量名 n' 的列表,因为 S 是一个单构造子。
作业难题
重写证明:
Theorem mult_n_1 : forall n : nat, n * 1 = n. Proof. intros n. rewrite <- mult_n_Sm. rewrite <- mult_n_O. reflexivity. Qed.对mult_n_Sm从右到左带入m=0
分类证明:遇到前提不对的情况下,用rewrite
Theorem andb_true_elim2 : forall b c : bool, andb b c = true -> c = true. Proof. intros b c H1. destruct b eqn:Eb. - destruct c eqn:Ec. + reflexivity. + rewrite <- H1. reflexivity. - destruct c eqn:Ec. + reflexivity. + rewrite <- H1. reflexivity.关于intros .
题目:
Theorem andb_eq_orb : forall (b c : bool), (andb b c = orb b c) -> b = c.如果是intro. simpl.只能对目标简化,不能简化到蕴含的前提,所以一开始不能将H intros


如果是intro b c.
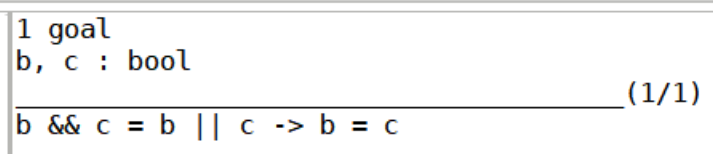


simpl.之后:
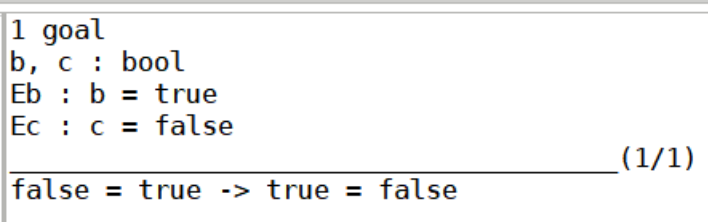
再intros . (即intros H.)

最终答案:
Proof. intros b c. destruct b eqn:Eb. - destruct c eqn:Ec. + simpl. reflexivity. + simpl. intros. rewrite -> H. reflexivity. - destruct c eqn:Ec. + simpl. intros. rewrite -> H. reflexivity. + simpl. reflexivity. Qed.notice :
Example test_bin_incr1 : (incr (B Z)) = A (B Z). Proof. simpl. reflexivity. Qed. (* 函数是会自己调的,Theorem才需要rewrite *)